Happy Birthday, Leonardo.

One positive aspect of staying in quarantine during the coronavirus pandemic has been finding more time to pursue my hobbies. This includes reading books with the most recent being the captivating biography Leonardo da Vinci by Walter Isaacson [1]. Isaacson synthesizes historical accounts and artifacts about Leonardo to present a coherent story of the famous Renaissance man's life, but what I more so appreciate is how Isaacson organizes the writing. He successfully humanizes Leonardo to the point that, while Leonardo lived hundreds of years ago, I can see him just as easily existing in today's world. Indeed, Leonardo was well ahead of his time. He designed tools and machines that would go on to be independently invented and built decades to centuries after his lifetime.

My reading of this book turns out to be timely: On this day 568 years ago, Leonardo da Vinci was born in Florence, Italy. And from that day till the day he died, Leonardo mastered a diverse portfolio of talents: drawing, engineering, architecture, geometry and anatomy, to name a few. While his breadth alone is impressive, Leonardo demonstrated his genius though his ability to combine his skills in new and exciting ways. Whether by applying his own anatomical studies to his method of painting the human body or by observing geometry and beauty in architecture, Leonardo ignored all preconceived boundaries between his areas of interest. This motivates what I believe are the core qualities that drove Leonardo's success.

1. He embraced his curiosity.
2. He explored connections that most other people weren't even thinking to consider.
3. He developed knowledge based upon his own experimentation: we don't often see theoretical conclusions in Leonardo's notebooks, but rather, conclusions based upon his observations.

If there's anything I would try to emulate from Leonardo's life, it would be these three guiding principles. In this post, we'll take a look at how Leonardo embodies them while examining a case study of his work on architecture. In true Leonardo fashion, we'll also take a hands-on approach of constructing our own arch and putting it to the test.

Architecture, Geometry and the Individual's Place in the Universe

While living in Milan, Leonardo began a study of architecture to guide his designs for new, grand churches. He applied his previously developed engineering knowledge combined with experimental observation to launch himself into this space in which he had no prior experience. This is a common theme in Leonardo's life.

Leonardo's personal taste in buildings was driven by the simple and elegant Florentine architecture which would later come to define the Renaissance style. Though this style was relatively new and transitional while the Gothic style was preeminent at the time. As a result, he failed on a few occasions to win over commissioners with his proposals, as oftentimes the more ornate Gothic style was preferred.

Leonardo collaborated with others such as Francesco di Giorgio in his architectural studies. Together, they turned to the classical text De Architectura (a.k.a. The Ten Books on Architecture), by Marcus Vitruvius Pollio, which asserts that the best buildings are those which are designed in accordance with the proportions of the human body. As only then, does the building take on a beauty symbolic of humanity's connection to the universe. In a practical vein, the book details the body's proportions for the benefit of architects wishing to put into practice his recommendations. Thus, Leonardo's study of Vitrivius' ideas led to one of his most well known drawings, Vitruvian Man.

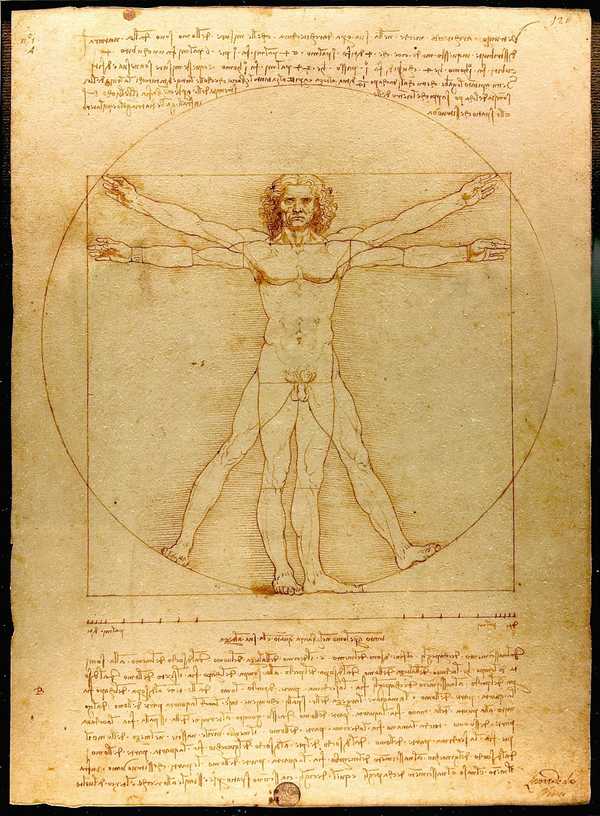
Vitruvian Man depicts an idealized man in one position superimposed on himself in another position. Surrounding his body is a circle and a square, both perfectly circumscribing the man. And in fact, the space between his legs (in the spread out position) roughly forms an equilateral triangle. The drawing is a graphical representation of Vitruvius' treatise but also a culmination of Leonardo's own anatomical expertise. The proportions Leonardo uses here are not those specified in De Architectura but rather those that come from his empirical study of human anatomy.

Ultimately, this drawing represents the epitome of Leonardo's qualities: curiosity through his study of De Architectura; finding connections through his combined application of drawing, geometry, architecture and anatomy; and empiricism through his revision of Vitruvius' proportions.

Strength in Arches

"The arch is nothing else than a force originated by two weaknesses…" - Leonardo da Vinci [2]

Leonardo went beyond considering the aesthetic qualities of a building; he additionally studied the structural integrity of architectural features like arches. And he did so in a delightful display of language. To see this, look to the quote above. Leonardo is stating that an arch is inherently strong by its geometrical design, but that it is only so when complete. Indeed, the rest of the quote reads

"…for the arch in buildings is composed of two segments of a circle, each of which being very weak in itself tends to fall; but as each opposes this tendency in the other, the two weaknesses combine to form one strength." [2]

He could have omitted the first half of the passage and still have maintained the meaning, yet the first half adds a poetic flair representative of his clarity of thought.

It's true that arches are effective at carrying weight over an opening (such as a door or a window). Since ancient times, arches have been used in architecture, and the Romans improved the technique through the use of "voussoir", or segmental wedges.

Arches form their strength through their ability to convert vertical forces into internal compression forces. This means that the voussoir in Roman arches increasingly compress against each other as weight is added on top. Precise analysis using force diagrams and equations of static equilibrium show how the vertical forces are thrust to the sides of the arch via compression. This strength of the arch then is conditional on counteracting the added thrust via heavy abutments (as in the above triumphal arch) at the sides of the arch or via ties, which you can see at the end of the post.

So, as strong as they are, arches still tend to fail in predictable ways. Leonardo detailed in his notebook (and I strongly encourage you check out his journal in its raw form with illustrations [3]) the ways in which arches tend to fail to a geometrical precision influenced by his observations and studies. For instance, he observes:

"An arch breaks at the part which lies below half way from the centre...If the excess of weight be placed in the middle of the arch at the point a, that weight tends to fall towards b, and the arch breaks at 2/3 of its height." [2]

When paired with his geometrical illustrations, his assertions as above form what historians consider may be the first precise, written account of architectural integrity. Today, such ideas have evolved into the field of civil engineering.

DIY Cardboard Arch

To enhance our appreciation of the ingenuity with which Leonardo approached architecture, I outline here my development of a fun project to construct an arch out of cardboard.

The planning phase began by considering the geometry. I wanted to build a semicircular (really a polygonal approximation) arch of a certain length and thickness from identical wedges as in the Roman voussoir. In addition, I wanted the template for each wedge to be constructed from a single piece of cardboard in order to better support itself in its assembled form. In the end, I decided upon a semi-octagon for no strong reason other than it seemed to be the simplest non-trivial approximation that would still resemble an arch.

Alas, a protractor / compass was missing from my arsenal, but a knowledge of trigonometry was not! Given an inner radius $r$, thickness $t$ and depth $d$, I developed a wedge template diagram.

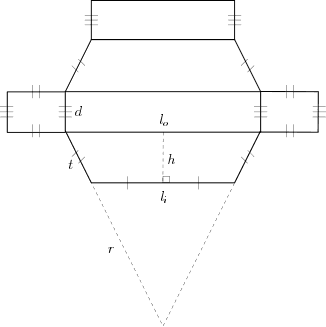
I then went on to solve for the perpendicular thickness $h$, the inner length $l_i$ and the outer length $l_o$. For the octagonal wedge, we have

My particular constraints of $r=5.25"$ and $t=d=2"$ yield $h = 1.8"$, $l_i=4"$ and $l_o=5.5"$.

The final semi-octagonal arch consists of three such full wedges and two half wedges. The beauty of an arch is that it is self-supporting, so there is no need to adhere the segments together — the natural geometry of the shape will reinforce its structure as weight is applied. This is conditional on ensuring we counter the natural thrust of the arch. You can do so by placing heavy objects at either side. I decided to to so by making use of a twine-based "tie" to counter the thrust via tension. What results is the photo at the beginning of this section.

Though I didn't push the arch to its limit, I was able to add around 15 pounds of weight to the arch before one of the outer wedges began to show signs of crushing into itself like a soda can (due to to the compressive forces which give the arch its strength). This signals the importance of the choice of material when building an arch. Cardboard does not have the compressive resistance that would, say, masonry as in the ancient arches of Leonardo's time.

From playing around with tension ties, lateral abutments, and various ways of distributing weight on the cardboard arch, I was able to bring to life the ideas from Leonardo's notebook. This is a fun and easy project, and I recommend it for anyone wanting to gain a stronger appreciation for Leonardo's excellence in geometry, art, engineering and architecture.

References

(1) Leonardo da Vinci, Walter Isaacson
(2) Leonardo's Journal on Architecture
(3) Leonardo's Journal with Illustrations